Object-oriented metrics by Robert Martin
- Processes, standards and quality
- Technologies
- Others
In 1994 Robert “Uncle Bob” Martin proposed a group of object-oriented metrics that are popular until now. Those metrics, unlike other object-oriented ones don’t represent the full set of attributes to assess individual object-oriented design, they only focus on the relationship between packages in the project.
The level of detail of Martin’s metrics is still lower than the one of CK’s metrics.
Martin’s metrics include:
- Efferent Coupling (Ce)
- Afferent Coupling (Ca)
- Instability (I)
- Abstractness (A)
- Normalized Distance from Main Sequence (D)
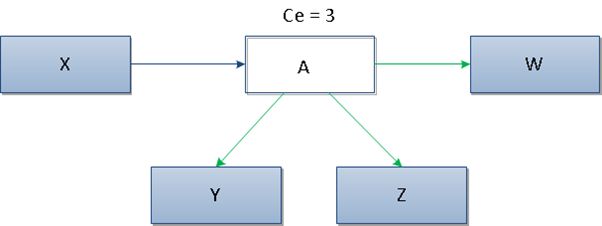
Efferent Coupling (Ce)
This metric is used to measure interrelationships between classes. As defined, it is a number of classes in a given package, which depends on the classes in other packages. It enables us to measure the vulnerability of the package to changes in packages on which it depends.
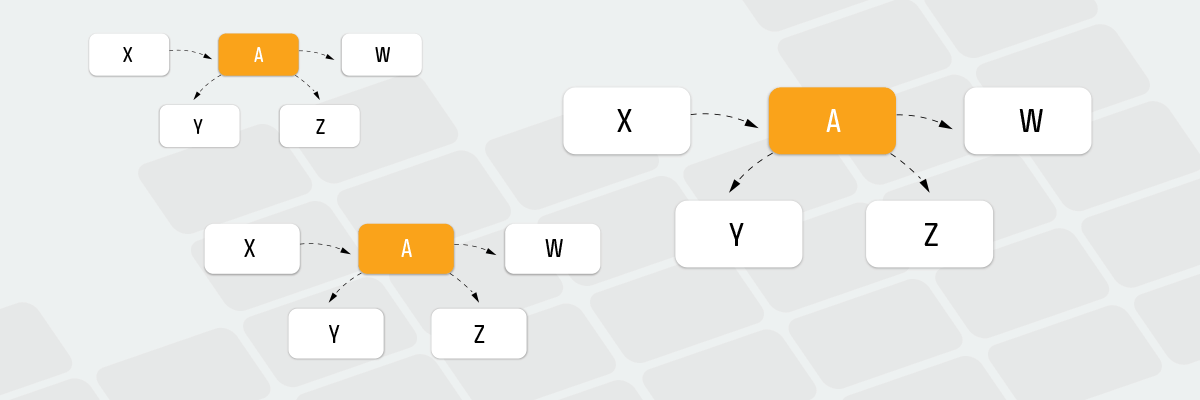
In the pic.1 it can be seen that class A has outgoing dependencies to 3 other classes, that is why metric Ce for this class is 3.
The high value of the metric Ce> 20 indicates instability of a package, change in any of the numerous external classes can cause the need for changes to the package. Preferred values for the metric Ce are in the range of 0 to 20, higher values cause problems with care and development of code.
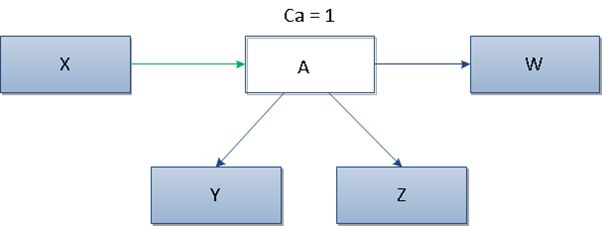
Afferent Coupling (Ca)
This metric is an addition to metric Ce and is used to measure another type of dependencies between packages, i.e. incoming dependencies. It enables us to measure the sensitivity of remaining packages to changes in the analysed package.
In the pic.2 it can be seen that class A has only 1 incoming dependency (from class X), that is why the value for metrics Ca equals 1.
High values of metric Ca usually suggest high component stability. This is due to the fact that the class depends on many other classes. Therefore, it can’t be modified significantly because, in this case, the probability of spreading such changes increases.
Preferred values for the metric Ca are in the range of 0 to 500.
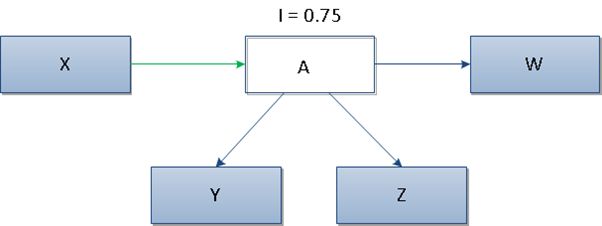
Instability (I)
This metric is used to measure the relative susceptibility of class to changes. According to the definition instability is the ration of outgoing dependencies to all package dependencies and it accepts value from 0 to 1.
The metric is defined according to the formula:
Where: Ce – outgoing dependencies, Ca – incoming dependencies
In the pic.3 it can be seen that class A has 3 outgoing and 1 incoming dependencies, therefore according to the formula value of metric I will equal 0,75.
On the basis of value of metric I we can distinguish two types of components:
- The ones having many outgoing dependencies and not many of incoming ones (value I is close to 1), which are rather unstable due to the possibility of easy changes to these packages;
- The ones having many incoming dependencies and not many of outgoing ones (value I is close to 0), therefore they are rather more difficult in modifying due to their greater responsibility.
Preferred values for the metric I should fall within the ranges of 0 to 0.3 or 0.7 to 1. Packages should be very stable or unstable, therefore we should avoid packages of intermediate stability.
Abstractness (A)
This metric is used to measure the degree of abstraction of the package and is somewhat similar to the instability. Regarding the definition, abstractness is the number of abstract classes in the package to the number of all classes.
The metric is defined according to the formula:
Where: Tabstract – number of abstract classes in a package, Tconcrete – number of concrete classes in a package
Preferred values for the metric A should take extreme values close to 0 or 1. Packages that are stable (metric I close to 0), which means they are dependent at a very low level on other packages, should also be abstract (metric A close to 1). In turn, the very unstable packages (metric I close to 1) should consist of concrete classes (A metric close to 0).
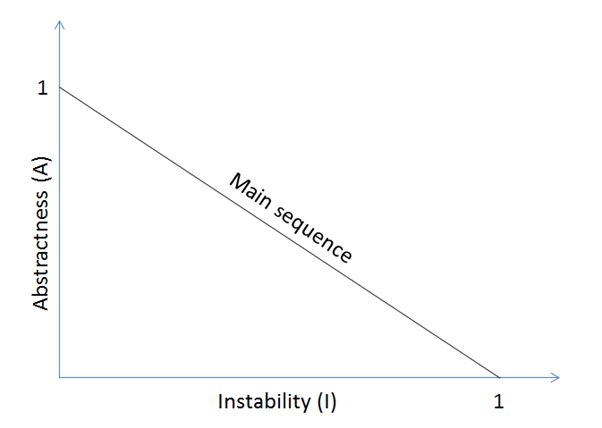
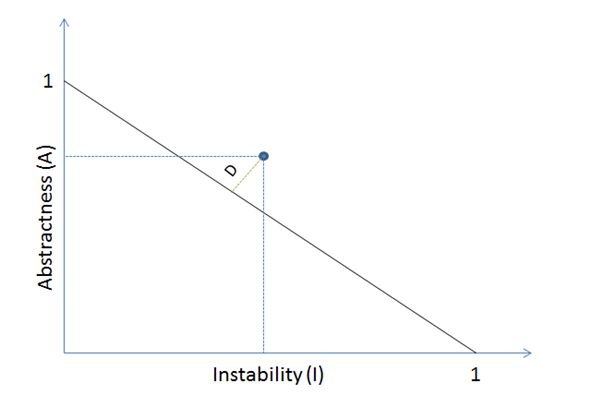
Additionally, it is worth mentioning that combining abstractness and stability enabled Martin to formulate thesis about the existence of main sequence (Pic. 4).
In the optimal case, the instability of the class is compensated by its abstractness, there is an equation I + A = 1. Classes that were well designed should group themselves around this graph end points along the main sequence.
Normalized Distance from Main Sequence (D)
This metric is used to measure the balance between stability and abstractness and is calculated using the following formula:
Where: A- abstractness, I – instability
The value of metric D may be interpreted in the following way; if we put a given class on a graph of the main sequence (Pic. 5) its distance from the main sequence will be proportional to the value of D.
The value of the metric D should be as low as possible so that the components were located close to the main sequence. In addition, the two extremely unfavourable cases are considered:
- A = 0 and I = 0, a package is extremely stable and concrete, the situation is undesirable because the package is very stiff and can’t be extended;
- A = 1 and I = 1, rather impossible situation because a completely abstract package must have some connection to the outside, so that the instance that implements the functionality defined in abstract classes contained in this package could be created.
Summary
Using Martin’s metrics we can easily assess the relationships between the packages in the project and determine whether it is necessary to carry out the changes so as to avoid any possible problems in the future. All metrics discussed in this article can be measured for projects in .NET using NDepend tool.