Splitting your secrets with Shamir’s Secret Sharing Scheme
- Processes, standards and quality
- Technologies
- Others
If you want to assure that your data is secure “at rest”, in 2018, you have a bunch of widely known and well-tested industry standards available on the market – such as symmetric/asymmetric cryptography, data vaults like keychain etc. But all these ideas struggle from threat called a single point of failure – if your master key is accessed by anyone, all data can be accessed in unencrypted form. How to mitigate this issue? Here is where Shamir’s Secret Sharing Scheme (referred later as SSSS) come into use.
Why should I use that?
A disgruntled employee, bribed administrator, lost access token, damaged servers – there are multiple ways to lose control over system secrets. Keys management is actually one of the most difficult aspects of information security, too often treated with nonchalance, by simple assumption “We’ll manage, duh, somehow”.
Probably the first solution that comes into your mind will be to split secret into parts, and give these parts to few (in example 8) “Key custodians” – people or servers that we trust, but not in full extent. Assume that our secret is 2048-bit long, randomly generated integer. Each of custodians will receive 256 bits (2048/8) of data to store – this will be named further as “shares”. To decrypt data each custodian must reveal his share. But what in case of failure – when, for example, one of the custodians dies in a traffic accident or one of the servers is attacked by ransomware? Data is lost and no one can extract it.
Thanks to Shamir’s Secret Sharing Scheme we can assure that secret will be recoverable even if one or more of custodians are not available. A number of shares needed to recover secret is configurable when shares are generated for the first time. New shares can be added without changing other shares.
How does it work?
But how it works? Taking out complicated finite field arithmetic and simplifying to integer arithmetic, citing Wikipedia article[1]:
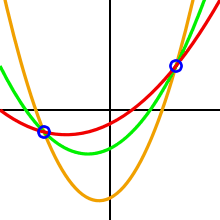
One can draw an infinite number of polynomials of degree 2 through 2 points.
3 points are required to define a unique polynomial of degree 2
If we define any parabola by defining parameters a, b and c of quadratic equation we are able to find an infinite number of points on such parabola. Now we can pass this generated values to our custodians. Because a number of points is infinite, we can create an infinite number of shares, but to recover this specific parabola, one needs to have access to at least three points (shares). Parameters of the generated parabola can be forgotten – they will be recoverable by simple math. And if we assume that free term of quadratic equation (parameter c) is application secret then this simple math allows us to recover application secret hidden in generated shares.
This is just a simplification – in fact, Shamir’s algorithm operates in the domain of finite field arithmetic. Because polynomials over a finite field are not representable on a 2-dimensional plane, finding solution requires more than plotting line through few points, but still, it is not so difficult to compute, even by hand.
Loss of trust in one of the custodians
To totally change shares (or invalidate one or more of the issued shares) without changing original data it is enough to generate new polynomial with the same free term.
Shares rotation can be used to improve security – an attacker cannot accumulate shares from multiple breaches, because shares are valid in batches, and only the latest batch is the valid one that can be used for secret restoration.
Unusual use case
Using SSSS it is possible to implement hierarchical resource access scheme. If we imagine company vault, holding secret data, locked using a pin code, we can split code using SSSS, with the assumption of, for example, 5 shares needed to recover code. Now we can give a different number of shares to different people:
- 5 shares for CEO,
- 4 shares for vice-president,
- 1 share for each executive.
Now CEO can get access to data alone, but at vice-president can access data only in cooperation with at least one executive. 5 executives are needed to unlock the vault.
Disadvantages
Unfortunately, at this moment, Shamir’s Scheme has some nuisances. First of all – this is only a concept, without any standardization. Although Adi Shamir released his paper[2] in 1979, up to now there is no codified set of rules that should be followed in implementation, so every architect and/or developer can introduce own improvements, making software less generic. If you want to download and use the library from your favourite repository, you will be probably limited to one or two not very popular libraries, that in fact should be checked by a person proficient in proving the security of algorithm from a mathematical point of view. This disadvantage, at first look, seems to be killer for the whole concept, but it is not. It is crucial to understand that fundament of data security is based on widely-known security standards – such as AES or RSA (which Adi Shamir co-authored), not SSSS itself. If you managed your keys in a secure way, SSSS will add an additional layer to your security stack, what is one of the concepts promoted by OWASP Security by Design Principles[3] – Principle of Defence in Depth.
Additionally paper does not provide any means to verify if custodians provided valid share, so every implementation can check output integrity differently, which greatly affects interoperability.
In my opinion, all of the mentioned disadvantages are not enough to overcome profits resulting from implementation of SSSS. It seems that big players trust SSSS too – for example, it is the algorithm of choice for HashiCorp Vault[4].
Proof of concept
Exemplary simple implementation of Shamir’s Secret Sharing Scheme in C# programming language can be found in my repository – https://bitbucket.org/bolek117/shamir-secret-sharing-scheme
[1] https://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing
[2] https://cs.jhu.edu/~sdoshi/crypto/papers/shamirturing.pdf
[3] https://www.owasp.org/index.php/Security_by_Design_Principles
[4] https://www.vaultproject.io/